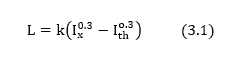Data obtained at Bell Labs by Kingsbury (1927) was the earliest to be used to generate loudness contour.

For many years, contours reported by Fletcher and Munson (1933) were used as the standard, but later contours were based on data obtained by Robinson and Dadson (1957). The latest revision of the ISO standard for loudness contours is evaluated by Suzuki and Takeshima (2004). The new contours are higher at low frequencies than those reported by Robinson and Dadson, so sounds at low frequencies must be more intense to be equal in loudness to those at 1 kHz and above. This means that there was overestimated by standards based on earlier data due to the contribution of low frequencies to the overall loudness of complex sounds.

The loudness function used in ISO 226 (2003) (International Organisation for Standardisation, 2003) is based on the threshold correction in (3.1), with an exponent of 0.27. This threshold correction is based on Hellman and Zwiclocki (1960) and Lochner and Burger (1961):

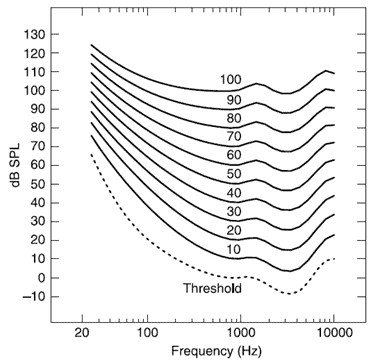
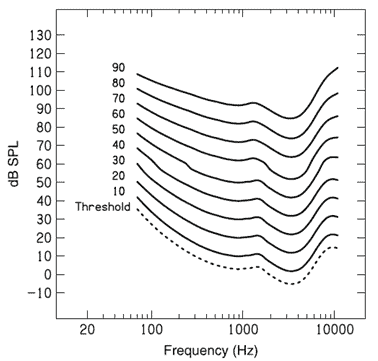
Equation (3.1) was chosen despite its prediction of zero loudness at threshold, because it had lesser parameters and gave more stable numerical solutions (Suzuki & Takeshima, 2004). The assumption of free-field conditions was adopted by ISO standard because that information is of greatest interest for engineering purposes, given that most people do not use headphones in everyday listening situations.The ANSI S3.4:2007 (American National Standards Institute, 2007) uses loudness model by Moore et al. (1997), but with the modified middle-ear transfer function described in Glasberg and Moore (2006) without incorporating binaural inhibition. This model assumes loudness simply sums across ears and loudness is computed for each ear and then added across ears. The loudness model is modified to include binaural inhibition in Moore and Glasberg (2007) and is described in ISO 532-2:2017 as there are evidence indicating that loudness does not simply sum across ears. Model for time-varying sound with binaural inhibition is described in ISO 532-3:2022. The ISO functions in Figure. 3.3 provide a more accurate description of loudness as a function of frequency than the ANSI functions in Figure.3.4, because the ISO functions were fitted to many sets of data where tones at different frequencies were matched in loudness. The ANSI standard, however, may provide a more accurate representation of the loudness growth function that provides a conversion from loudness level in phons to loudness in sones (Florentine et al., 2011).
 

Figure 3.3 : Loudness contour as described by ISO 226:2003 standard.

Note. From Loudness p. 118 by Florentine, M., Popper, A. N., & Fay, R. R. (Eds.). (2011). Springer New York
 

Figure 3.4: Loudness contours predicted by ANSI S3.4 (2007) standard, as modified by Glasberg and Moore (2006). The contours were generated using software developed by Brian Glasberg distributed with the ANSI standard

Note. From Loudness p. 120 by Florentine, M., Popper, A. N., & Fay, R. R. (Eds.). (2011). Springer New York.
 
 
 
Moore, B. C. J., & Glasberg, B. R. (2002). A Model of Loudness Applicable to Time-Varying Sounds

Moore, B. C. J., & Glasberg, B. R. (2007). Modeling binaural loudness. Journal of Acoustic Society of America, 121, 1604-1612. https://doi.org/10.1121/1.2431331

Moore, B. C. J., Glasberg, B. R., & Schlittenlacher, J., Ellermeier, W. (1997). A Model for the Prediction of Thresholds, Loudness, and Partial Loudness. Journal of Audio Engineering Society, 45(4), 224-240. https://www.aes.org/e-lib/browse.cfm?elib=10272

Moore, B. C. J., Glasberg, B. R., , & Stone, M. A. (2003). Why Are Commercials so Loud? — Perception and Modeling of the Loudness of Amplitude-Compressed Speech. Journal of the Audio Engineering Society,, 51(12), 1123-1132. https://www.researchgate.net/publication/288727864_Why_Are_Commercials_so_Loud_-_Perception_and_Modeling_of_the_Loudness_of_Amplitude-Compressed_Speech
 
Lochner, J., & Burger, J. F. (1961). Form of the loudness function in the presence of masking noise. Journal of Acoustic Society of America. https://doi.org/10.1121/1.1908548
 
Fletcher, H., & Munson, W. A. (1933). Loudness, its definition, measurement, and calculation. Journal of Acoustic Society of America, 5, 82-108.
 
Florentine, M., Popper, A. N., & Fay, R. R. (2011). Loudness. Springer New York https://doi.org/10.1007/978-1-4419-6712-1
 
Robinson, D. W., & Dadson, R. (1957). Threshold of Hearing and Equal-Loudness Relations for Pure Tones, and the Loudness Function. The Journal of the Acoustical Society of America, 29(12), 1284-1288. https://doi.org/10.1121/1.1908766
 
Suzuki, Y., & Takeshima, H. (2004). Equal-loudness-level contours for pure tones. The Journal of the Acoustical Society of America, 116(2), 918-933. https://doi.org/10.1121/1.1763601
 
Hellman, R., & Zwiclocki, J. (1960). On some factors affecting the estimation of loudness. The Journal of the Acoustical Society of America, 32, 924. https://doi.org/10.1121/1.1936488
 
International Organisation for Standardisation. (2003). ISO 226:2003 Acoustics — Normal equal-loudness-level contours.
 
International Organisation for Standardisation. (2017). ISO 532-1:2017 Acoustics — Methods for calculating loudness — Part 1: Zwicker method
 
International Organisation for Standardisation. (2017). ISO 532-2:2017 Acoustics — Methods for calculating loudness — Part 2: Moore-Glasberg method
 
International Organisation for Standardisation. (2023). ISO 532-3:2023 Acoustics — Methods for calculating loudness — Part 3: Moore-Glasberg-Schlittenlacher method
 
American National Standards Institute. (2007). ANSI S3.4-2007: Procedure for the Computation of Loudness of Steady Sounds